Breaking the Curse of Dimensionality (Locally) to Accelerate Conditional Gradients
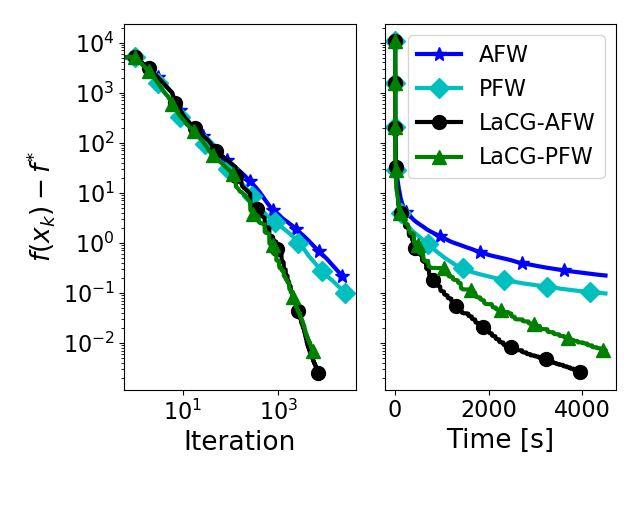 Primal gap convergence comparison: Minimization of quadratic over the convex hull of MIPLIB polytope (ran14x18-disj-8). See paper for details.
Primal gap convergence comparison: Minimization of quadratic over the convex hull of MIPLIB polytope (ran14x18-disj-8). See paper for details.
Abstract
Conditional gradient methods constitute a class of first order algorithms for solving smooth convex optimization problems that are projection-free and numerically competitive. We present the Locally Accelerated Conditional Gradients algorithmic framework that relaxes the projection-freeness requirement to only require projection onto (typically low-dimensional) simplices and mixes accelerated steps with conditional gradient steps to achieve dimensionindependent local acceleration for smooth strongly convex functions. We prove that the introduced class of methods attains the asymptotically optimal convergence rate. Our theoretical results are supported by numerical experiments that demonstrate a speed-up both in wall-clock time and in per-iteration progress when compared to state-of-the-art conditional gradient variants.