CGINDy: Conditional gradient-based Identification of Non-linear Dynamics - Submitted to the Journal of Computational and Applied Mathematics
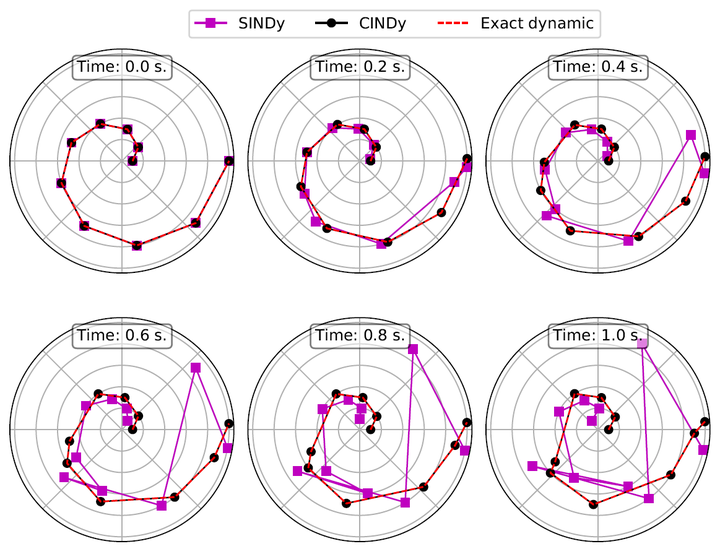 Kuramoto dynamic: Comparison of the dynamic learnt by CINDy, and SINDy from noisy data coming from the Kuramoto dynamic. The exact dynamic is shown with a dashed red line.
Kuramoto dynamic: Comparison of the dynamic learnt by CINDy, and SINDy from noisy data coming from the Kuramoto dynamic. The exact dynamic is shown with a dashed red line.
Abstract
Governing equations are essential to the study of nonlinear dynamics, often enabling the prediction of previously unseen behaviors as well as the inclusion into control strategies. The discovery of governing equations from data thus has the potential to transform data-rich fields where well-established dynamical models remain unknown. This work contributes to the recent trend in data-driven sparse identification of nonlinear dynamics of finding the best sparse fit to observational data in a large library of potential nonlinear models. We propose an efficient first-order Conditional Gradient algorithm for solving the underlying optimization problem. In comparison to the most prominent alternative algorithms, the new algorithm shows significantly improved performance on several essential issues like sparsity-induction, structure-preservation, noise robustness, and sample efficiency. We demonstrate these advantages on several dynamics from the field of synchronization, particle dynamics, and enzyme chemistry.