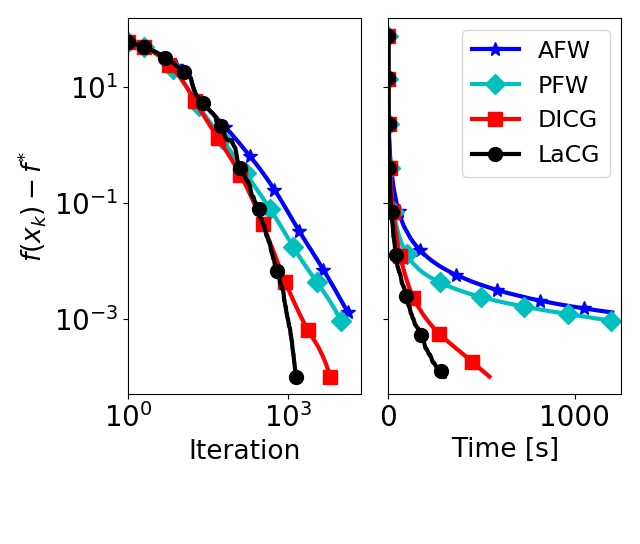
 Primal gap convergence comparison: Minimization of quadratic over Birkhoff polytope. See paper for details.
Primal gap convergence comparison: Minimization of quadratic over Birkhoff polytope. See paper for details.
Abstract
Conditional gradients constitute a class of projection-free first-order algorithms for smooth convex optimization. As such, they are frequently used in solving smooth convex optimization problems over polytopes, for which the computational cost of orthogonal projections would be prohibitive. However, they do not enjoy the optimal convergence rates achieved by projection-based accelerated methods; moreover, achieving such globally-accelerated rates is information-theoretically impossible for these methods. To address this issue, we present Locally Accelerated Conditional Gradients – an algorithmic framework that couples accelerated steps with conditional gradient steps to achieve local acceleration on smooth strongly convex problems. Our approach does not require projections onto the feasible set, but only on (typically low-dimensional) simplices, thus keeping the computational cost of projections at bay. Further, it achieves the optimal accelerated local convergence. Our theoretical results are supported by numerical experiments, which demonstrate significant speedups of our framework over state of the art methods in both per-iteration progress and wall-clock time.