Second-order Conditional Gradient Sliding - Fields Institute Communication Series on Data Science and Optimization
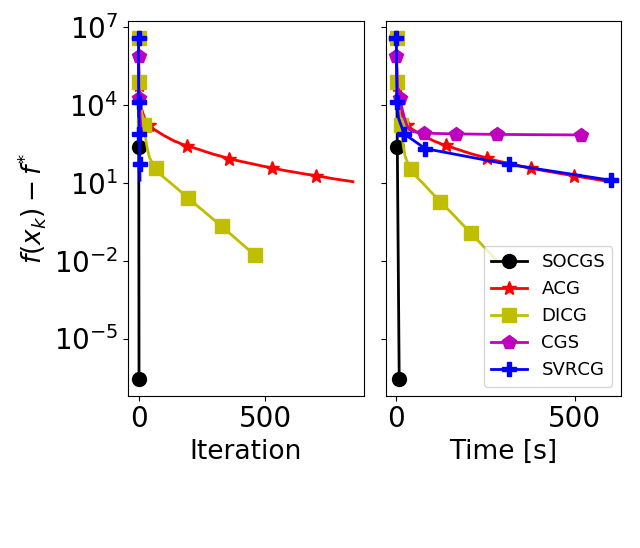 Primal gap convergence comparison: Sparse coding over Birkhoff polytope. See paper for details.
Primal gap convergence comparison: Sparse coding over Birkhoff polytope. See paper for details.
Abstract
Constrained second-order convex optimization algorithms are the method of choice when a high accuracy solution to a problem is needed, due to their local quadratic convergence. These algorithms require the solution of a constrained quadratic subproblem at every iteration. We present the Second-Order Conditional Gradient Sliding (SOCGS) algorithm, which uses a projection-free algorithm to solve the constrained quadratic subproblems inexactly. When the feasible region is a polytope the algorithm converges quadratically in primal gap after a finite number of linearly convergent iterations. Once in the quadratic regime the SOCGS algorithm requires $\mathcal{O}(\log(\log 1/\varepsilon))$ first-order and Hessian oracle calls and $\mathcal{O}(\log (1/\varepsilon) \log(\log1/\varepsilon))$ linear minimization oracle calls to achieve an $\varepsilon$-optimal solution. This algorithm is useful when the feasible region can only be accessed efficiently through a linear optimization oracle, and computing first-order information of the function, although possible, is costly.