Biography

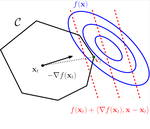
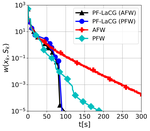
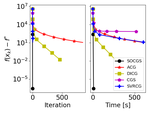
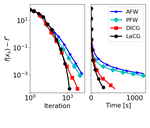
I am a Quantitative Researcher at Quantfury, working in Machine Learning techniques for algorithmic trading. I obtained my Ph.D. in Machine Learning at the Georgia Institute of Technology, working with Prof. Sebastian Pokutta, on designing novel convex optimization algorithms with solid theoretical convergence guarantees and good numerical performance.

Prior to joining the Ph.D. program I worked at HP as an R&D Systems Engineer for two years. I obtained a bachelor of science in Industrial Engineering from the Universidad Politécnica de Madrid and a Master of Science in Applied Physics from Cornell University.